One code to rule them all. One code to implement them all, and in the same framework bind them.

In the feature engineering of any data related project, we often have to filter the columns we will use to train our model manually; this filtering often relies on the insights we have on data and also on many criteria that can help us distinguish between the valuable attributes and the redundant or the meaningless ones, this process is known as the feature selection.

They are many different ways of selecting attributes; the one we see today is known as the ranking feature selection. It’s the most basic way. It evaluates each attribute with a function, ranks them and keeps the best attributes.

Although this ranking can be done with various methods, we will explore these method’s classification, see how this classification can help us organize them into a reliable and extensible framework, and use this framework to test and compare their behaviours.

Feature selection ranking methods

In feature selection, we can classify the quality measure of an attribute into five categories according to the classification made by Dash and Liu.

• Distance measures: These quantify the correlation between the attributes and the label.
• Information measures: These information theory measures are interested in the label’s entropy after splitting them according to a feature's value.
• Consistency measures: A feature is consistent if the same values are not associated with different values of the class.
• Dependency measures: Two variables are said to be independent if the probability of taking a specific value is not influenced by information on the other's value, so these measures work by quantifying the class's dependency on an attribute.
• Classification measures: These measures are time expensive; they evaluate the classification quality when taking a specific attribute.

I will, of course, come back to each of these classes when presenting the measures I will consider.

Conception baseline

Before defining our functions, we need to set a clear and scalable baseline that will dictate further development.

To use it, we need to isolate the different components we’ll need to build our framework; the modelisation I propose is based on three key notions:

• Measure: A measure quantifies a relationship between two vectors; this relationship can be related to the dependence, the independence or the correlation between them.Feature selection ranking methods
• Evaluation Function: An evaluation function evaluates the importance of a feature by using a measure; an evaluation can be bounded to a single measure for mutual information evaluation or correlation evaluation or modulable to different measures for classification measures that depend on the classifier we consider.
• Feature Selection Function: A feature selection function takes the whole dataset and performs the feature selection either by ranking the dataset's features and taking a percentage or by making an incremental selection, as we’ll see later.

Now, let’s enumerate the main functionalities of each category of components because this will give us what we’ll have to put on the top of our architecture:

• Measure: A function can model the measure since it doesn't need to preprocess the data; it simply computes a value that will be interpreted and used by highly placed components.
• Evaluation function: Here we may have a preprocessing since we must take into account that some evaluation function requires categorical features, this class of components will then be split into two kinds depending on their need to a discretisation function, a part of that, the leading utility of each evaluation function is to evaluate the importance of a feature regarding the class.
• Feature Selection Function: This will be an abstract interface that provides the end-user access to the method “select”, which selects a given number of features, and will be implemented by many subclasses depending on the method you want to use for the selection.

All we have to do now is to develop our architecture from top to bottom and link it to our measurements; this gave me the following architecture.

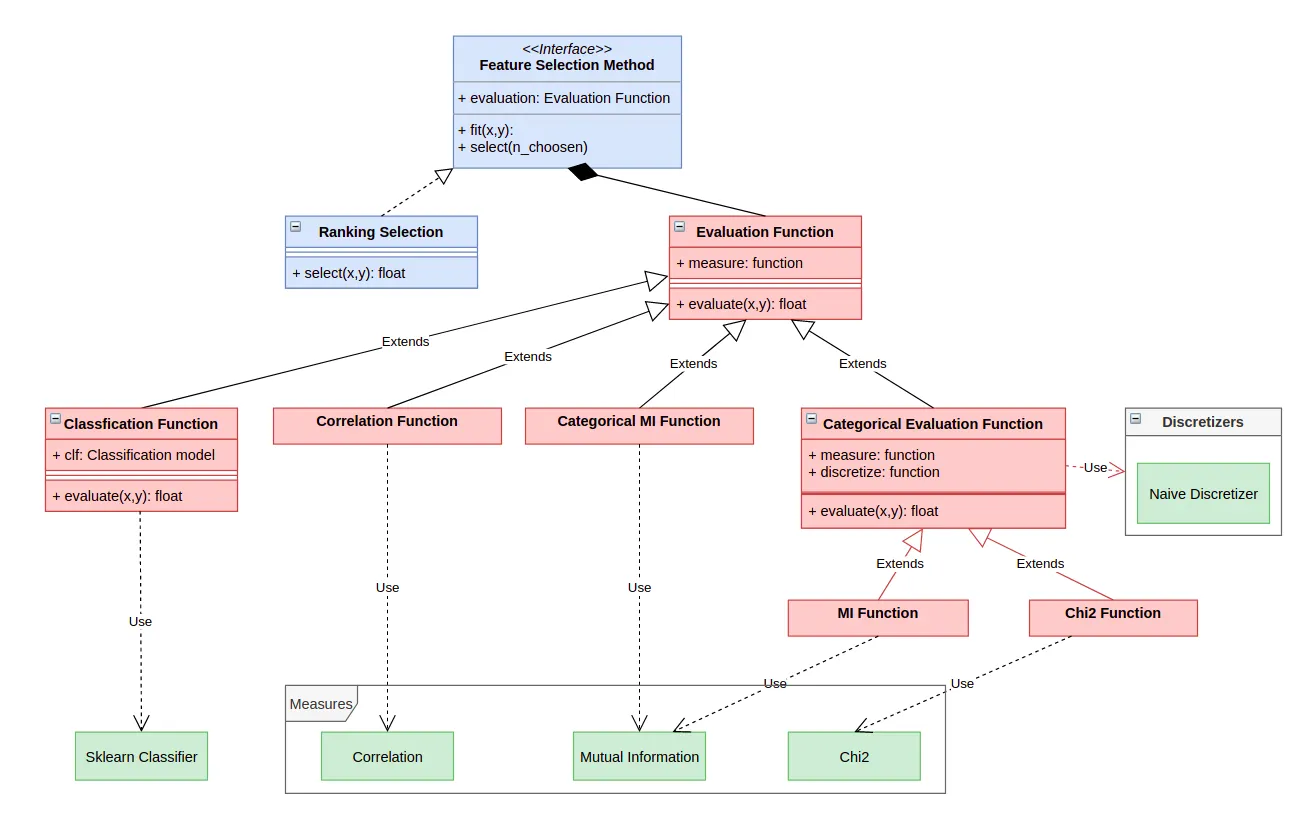
Reliability test

To assess the reliability of our framework and especially when adding a new measure, we have to think of an integrity test to run each time we’ll add an evaluation function; this test has to be the more generic possible and to do so, we will adopt a convention, from now on every evaluation function class have to contain the word “Function” in his name.

By doing this, we can elaborate a simple test that runs as following: for each evaluation function class it founds in the file “evaluation_functions.py”, it will try to rank the features of a random dataset to verify that all the evaluation functions are well written.

Of course, it’s simple provided that we have a way for inspecting the script and dynamically instantiate objects with the classes in it, and we can do this by using the inspect module.

from inspect import getmembers, isclassfrom sklearn.datasets import make\_classificationfrom core.Feature\_Selection import Evaluation\_Functionfrom core.Feature\_Selection.Ranking\_Function import Ranking\_SelectionX,y = make\_classification(n\_samples=1000, n\_features=10, n\_classes=2)for i, j in (getmembers(Evaluation\_Function, isclass)):if("Function" in i and not "CAT" in i):print("Testing: ",i, end=" ")EF = j()R = Ranking\_Selection(j())c = R.fit(X, y)print("✓")

These few lines will create a dataset of 10 features and 1000 samples, and the get_member method will inspect the Evaluation_Function script, and for each class in it with “Function” in its name, we will perform a ranking selection and print a tick when it’s done.

Used measures

The main advantage of using a framework is its extensivity, but for now, I linked the following functions; I won't go into the details of each measure; I will take just precise their classes and a high-level description of how they evaluate features:

• Pearson Correlation Coefficient(from NumPy) is a distance measure that can be obtained by calculating the ratio of covariance between the two variables.
• Signal based correlation(from NumPy) it’s another measure of correlation that is implemented in NumPy.
• Mutual information(from Scikit-learn) it’s an information measure that evaluates the attribute by measuring the diminution of entropy in the class if we split it with respect to his values.
• Chi2 Independence Test(from Scikit-learn) two variables are independent if P(X=x; Y=y) = P(X=x). P(Y=y), by performing a Chi2 test on this hypothesis between an attribute and the class, we can quantify its importance.
• Classification Measures: as a classification measures, to evaluate each attribute, I trained a classifier with the dataset restricted to this particular attribute and, after that, measured its accuracy; since the classifier is given as a parameter, I tried this measure with a Decision Tree Classifier and then I also added a Logistic Regression Classifier.

Keep in mind that this blog's point is not implementing these methods, so I took already implemented quality measures.

Performance test

Each time we implement a new evaluation function, we are not interested only in its compliance with the framework. We also want to evaluate its efficiency;

So after the integrity test, we will design two simple performance test; the first test consists of the following:

• We create a dummy dataset with k relevant features.
• We train a classifier with the whole dataset and evaluate its accuracy.
• For each function, we select k features and train the classifier with the dataset restricted to the selected features and evaluate the classifier's accuracy with a k-fold validation.

And the second one is pretty similar, but instead of generating a full-random dataset, we will take the iris dataset and add to it randomly sampled columns.

Each test is done 10 times, and the time is measured for each evaluation function.

For the first test with twenty attributes and only five informative attributes, we obtained the following results on an SVM classifier:

base : 0.8974500000000001 Time: 0.0CHI2\_Function : 0.52885 Time: 0.017551565170288087CorrelationSP\_Function : 0.7693999999999999 Time: 0.00019888877868652345Correlation\_Function : 0.8606 Time: 0.0020094394683837892DTClassification\_Function : 0.6241 Time: 0.09251418113708496MI\_Function : 0.89475 Time: 0.1389768123626709

The base indicates the accuracy obtained by keeping all the attributes. We can notice that we kept almost the same performance for the mutual information by reducing the number of attributes by 80%; we also notice that the CHI2 function is almost useless, but it can be because it’s especially altered by the naive binarization I used which consists simply on dividend the range of the data to equally spaced intervals.

Let’s consider another example with a full random dataset, this time we’ll take 200 features (for only 2000 samples) and 50 informative ones, we obtain these results :

base : 0.7943999999999999 Time: 0.0CHI2\_Function : 0.46049999999999996 Time: 0.171110200881958Correlation\_Function : 0.8112499999999998 Time: 0.019919610023498534DTClassification\_Function : 0.60955 Time: 0.9978075504302979MI\_Function : 0.8505000000000001 Time: 1.4385223627090453

Again, we can see that Mutual information keeps very relevant attributes, so much that it even beat the classification with all the variables.

Now let’s see the second test,

base : 0.9086666666666667 Time: 0.0CHI2\_Function : 0.946 Time: 0.01797773838043213CorrelationSP\_Function : 0.9740000000000001 Time: 0.00014123916625976562Correlation\_Function : 0.9693333333333334 Time: 0.0030328035354614258DTClassification\_Function : 0.3539999999999999 Time: 0.020097732543945312MI\_Function : 0.9493333333333334 Time: 0.091739821434021

This time, all the measures a part of the classification measure perform better than the base, which confirms that a ranking measure's efficiency is strongly related to the dataset's structure.

A more trustworthy way of comparing ranking methods

Since the principal advantage of ranking methods is that they are not time expensive, we could generate the ranking and then evaluate the subsets obtained by successively adding the features from the top of the ranking to the bottom.

We obtain by using Seaborn and the dataset IRIS with added useless columns the following plot.

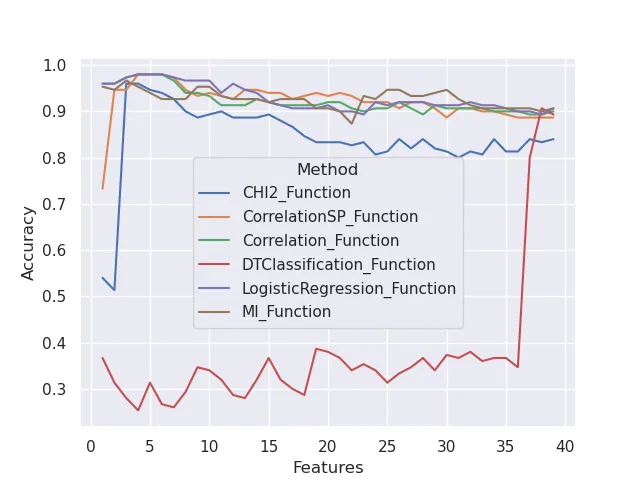
This confirms that:

• The classification with a decision tree is not a valid ranking method for this dataset.
• The number of useful features seems to be 4 since all the ranking methods give their higher performances for around 4 features.

Conclusion:

Since a ranking method is not (in general) time expensive, we can use many ranking methods to obtain better insights into our feature’s quality if we have a reliable framework.

This framework also allows us to try new evaluation functions or new selection mechanisms, which I encourage you to do by forking my GitHub repo.

Open Question:

This framework opens a new question: Can we exploit the fact that we have many rankings of the features? I have a little idea on the answer; keep in touch to discover it soon :)

Feel free to join me by mail (ouaguenouni.hachemi@gmail.com) or on LinkedIn if you want to debate this topic.